L’informatique quantique inaugure une révolution technologique, offrant des capacités de calcul spectaculaires et transformant radicalement des domaines comme la cryptographie et la recherche scientifique. Préparez-vous à un avenir où les limites de l’innovation sont repoussées comme jamais auparavant.
Introduction au quantique
Les machines quantiques sont des prouesses technologiques, elles exploitent des objets quantiques afin de réaliser des algorithmes quantiques. Cependant, ces machines sont très complexes à construire et encore plus à utiliser. En effet les processeurs quantiques sont utilisables à -270° C, et donc le nombre d’erreurs de ces processeurs sont encore très élevés.
Qu’est-ce qu’un processeur quantique?
Les processeurs quantiques sont composés d’objets quantiques, comme des photons par exemple. On appelle ces objets des qubits, c’est en mesurant ces qubits qu’on est capable d’effectuer des calculs. On mesure la puissance d’un ordinateur quantique en nombre de qubits. Plus le nombre de qubits est élevé, plus l’ordinateur est supposé être performant. A l’heure actuelle, les plus puissants possèdent autour de 1000 qubits.
Les qubits
Mais revenons un peu aux qubits. Il existe plusieurs types de qubits et plusieurs technologies d’informatique quantique. La plus utilisée est la plus populaire actuellement étant le qubit à base de supraconducteurs plus simple à manipuler que les autres types de qubits mais fonctionnant à très basse température. Un qubit peut avoir deux états : soit 0 soit 1. Un exemple d’interprétation serait la rotation d’une particule quantique, de quel côté la particule tourne définis une binarité. Les qubit sont aussi sujets à plusieurs propriétés de la physique quantique. Voici les deux propriétés qu’on utilisera le plus régulièrement dans l’informatique quantique :
- La superposition quantique : Un qubit en superposition quantique n’a plus d’état fixe. On ne connait plus son état (|0> ou |1>), il peut devenir chaque état avec certaines probabilités. Tant qu’on ne l’observe pas l’objet quantique reste dans un état inconnu.
- L’intrication quantique : Lorsque deux objets quantiques sont intriqués, ils sont connectés entre eux. Chaque modification d’un qubits influe sur l’autre qubit intriqué instantanément et peu importe la distance.
Maintenant que les qubits sont présentés, nous pouvons discuter de comment est-il possible de modifier les qubits pour faire de l’informatique quantique ?
Portes et Circuit quantique
Afin de modifier les états des qubits, il existe des portes quantiques qui permettent d’effectuer des changements sur les états des qubits, pour être plus exact les portes quantiques changent des probabilités d’apparition des états quantiques en superposition.
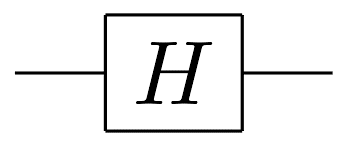
Porte Hadamard (permet de mettre le qubit en superposition)
Rassemblées, on dit que ces portes quantiques forment un circuit quantique. Ces circuits ne restent que des représentations afin de réaliser des algorithmes. Chaque porte est un phénomène physique qui modifie le qubits, ces phénomènes dépendent de la technologie utilisée. En effet, il n’existe pas de circuit quantique comme des circuits électroniques. Les portes quantiques sont une modélisation des actions faites sur les qubits, elles sont là pour comprendre et traduire les algorithmes en un langage informatique. On peut cependant, grâce aux portes quantiques, réaliser toutes les opérations logiques classiques tout en exploitant des propriétés intrinsèques des qubits. L’un des meilleurs exemples de l’exploitation de ces propriétés est l’algorithme QAOA. Cet algorithme exploite une méthode de mesure d’énergétique, il n’est plus question de binarité mais de mesure de valeur réel. L’informatique quantique consiste à créer le circuit quantique qu’on va effectuer sur les qubits.
Utilisation dans un cadre réel
La plupart des grands algorithmes quantiques ont été créés grâce à des représentations mathématiques. Le principe est simple, on part d’un état précis des qubits puis on représente mathématiquement l’effet des portes quantiques sur les qubits et on cherche à tomber sur le bon résultat. Après cette construction de circuit, on teste notre circuit et on observe le résultat. Comme en informatique classique le résultat et les paramètres d’entrée sont une suite de 0 et de 1 (représentée par des qubits). A cause de la superposition quantique qui est présente dans tous les algorithmes, le résultat est probabiliste. On peut avoir un mauvais résultat après itération de l’algorithme comme un bon résultat et cela dépend de la probabilité d’apparitions des états après utilisation du circuit quantique. Les circuits quantiques sont à l’origine des limitations des machines quantiques actuelles. A chaque itération de porte, on a une chance de modifier le résultat de manière définitif (i.e. de commettre une erreur de calcul), donc plus un circuit possède de portes moins il est réalisable sur machine réelle.
L’informatique quantique à l’heure actuelle
A l’heure actuelle, le meilleur ordinateur quantique est surement chez IBM avec plus de 400 qubits. Cela reste très limité à cause de l’erreur associée à ces machines. Même si le nombre de start-up possédant des ordinateurs et l’investissement augmentent grandement chaque année, les ordinateurs quantiques sont peu nombreux. Ces ordinateurs ne sont en plus pas tous accessibles au public. Pour pouvoir tester les algorithmes et analyser les résultats, les grosses entreprises ont mis en place des simulateurs d’informatique quantique. Ces simulateurs vont reproduire le comportement des qubits (sans l’erreur) et c’est ce qui permet de tester la plupart des algorithmes quantiques sans disposer d’une machine dédiée.
Algorithmes
Comme montré précédemment, les machines quantiques sont des machines au fonctionnement complexe, difficile à construire et encore imparfaites. Des questions émergent alors assez facilement : Pourquoi investir dans le quantique ? Le quantique pourra-t-il avoir des cas d’usages à court terme ? Quels avantages présente l’informatique quantique ? Afin de répondre à ces questions, notre étude a porté sur deux algorithmes très populaires, l’algorithme de Grover et l’algorithme QAOA.
Grover
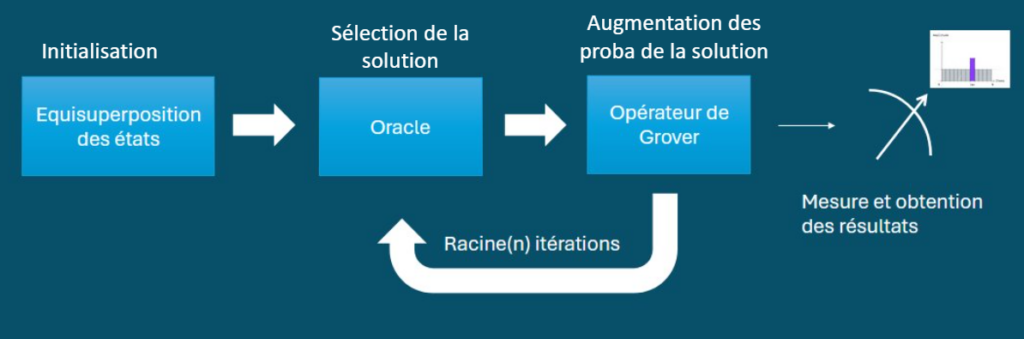
Nous avons choisi comme premier algorithme, l’algorithme de Grover. C’est un algorithme qui a été théorisé dans les années 1990, et qui a pu être testé depuis dans le cadre réel. Cet algorithme a pour objectif la recherche en base de données, il permet d’avoir un gain quadratique par rapport à un algorithme classique. Ce gain en complexité temporelle peut sembler certes négligeable mais devient indispensable pour réaliser des opérations complexes sur d’énormes bases de données. On peut penser à certains calculs ou à du préprocessing de données en Intelligence Artificielle. Cet algorithme représente la première façon de réaliser de l’informatique quantique, il est à la fois très prometteur d’un point de vue gain mais aussi trop difficile à implémenter sur machine réel à l’heure actuelle. Dans un sens c’est un algorithme de la même gamme que le célèbre algorithme de Shor (encore impossible mais révolutionnaire). Pour vulgariser le fonctionnement de cet algorithme, on peut le diviser en plusieurs partie, comme sur ce schéma :
Représentation schématique de l’algorithme de Grover
L’algorithme va augmenter la probabilité de tomber sur le bon résultat au fur et à mesure des itérations. La complexité de cet algorithme repose sur la création de “l’Oracle”. Une Oracle est un opérateur rempli de portes logiques qui permet de d’isoler l’état solution. Cette “boîte noire” dépend de chaque sujet et comporte énormément de portes logiques si on veut sélectionner des éléments de manière complexe. Notre POC portait sur une application directe de l’algorithme : l’application dans le cadre d’un système de recommandation. Voici un exemple connu d‘algorithme de recommandation : lorsqu’un réseau social vous propose le profil d’une personne qui pourrait être en adéquation avec le vôtre (Facebook, LinkedIn). Même si cela peut paraître simple, afin de réaliser ce système de recommandation en quantique, on est obligé de réaliser trois oracles différents. On peut cependant trouver un défaut à l’algorithme de Grover: la fabrication des oracles, non triviale et qui nécessite une quantité de portes logiques très élevée pour réaliser des opérations complexes. C’est d’ailleurs pour cette raison que les recherches actuelles se concentrent sur d’autres algorithmes dits “algorithmes variationels quantiques” comme l’algorithme QAOA, plus faciles à mettre en place.
QAOA
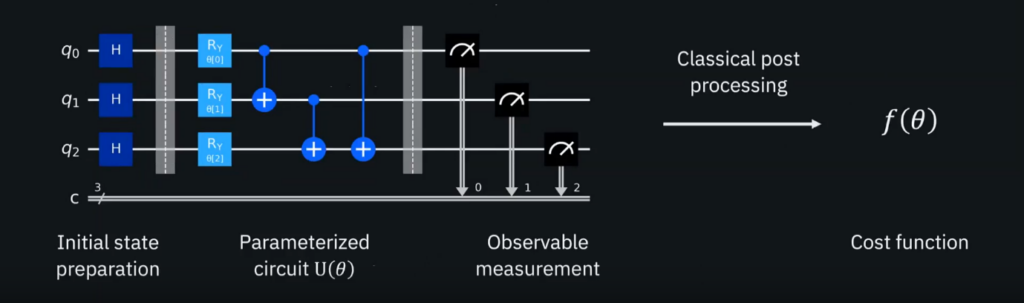
QAOA n’est pas un algorithme comme les autres, c’est une méthode pour résoudre des problèmes mathématiques. Les problèmes en question sont les problèmes QUBO, ce sont des problèmes de minimisation d’une fonction quadratique associé à un graph. Le fonctionnement de cet algorithme est très différent des autres algorithmes classiques. Il repose sur deux propriétés physiques des qubits. On a vu précédemment que les qubits étaient binarisés mais dans le cadre de cet algorithme ce n’est pas tout à fait vrai. Comme le problème à résoudre est un problème de minimisation, l’algorithme exploite l’énergie des qubits pour sa résolution. Ainsi on rentre la modélisation du problème dans le circuit, puis on minimise l’énergie du circuit. L’objectif est d’optimiser le circuit en analysant sont énergie. Pour être sûr que cela fonctionne, on exploite le théorème adiabatique quantique qui permet de trouver la solution. Ce théorème dit qu’en modifiant suffisamment lentement un objet quantique, celui-ci reste dans le même état énergétique. On utilise ce principe en modélisant un problème simple dans les qubits avec une énergie minimale, puis on modifie les qubits lentement pour qu’ils modélisent notre problème. Ainsi les qubits à la fin du processus représenteront la solution qui minimise l’équation du problème.
Représentation schématique de l’algorithme de QAOA
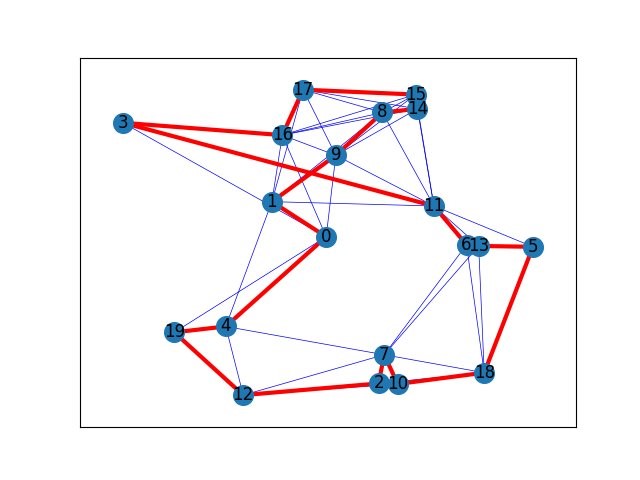
Même si cet algorithme est très complexe à vulgariser il représente une avancée majeure dans le domaine. Afin de vous donner quelques repères, cet algorithme peut être utilisé dans la problématique du voyageur de commerce : algorithme pouvant permettre d’optimiser le chemin d’un livreur ou postier. Ce problème est un problème classique de graph ou l’objectif est de minimiser la distance d’un voyage d’un point A à un point B en prenant en compte les étapes intermédiaires. Sur le graph ci-dessous le chemin résolvant le problème est annoté en rouge :
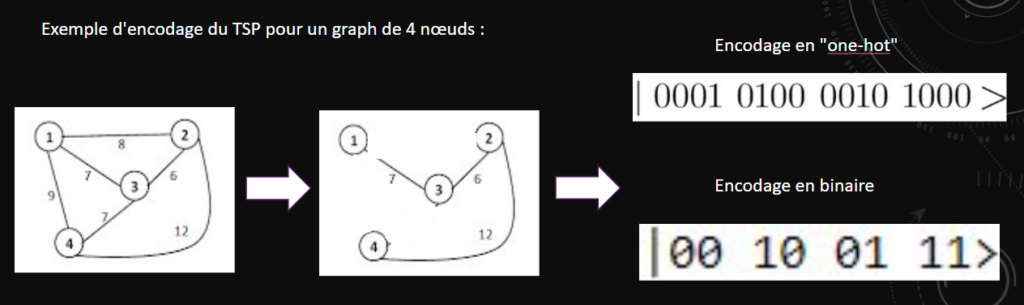
Cet algorithme a pour objectif d’être utilisable à l’heure actuelle avec un gain sur machine réelle et offre réellement des gains des performances sur des problèmes pratiques et complexes à résoudre. QAOA est néanmoins très récent et présente certains défauts qui compliquent son utilisation dans un cadre réel, on peut citer notamment la problématique de l’encodage des données d’entrées. Cette limite en cadre réel est dû à la modélisation du problème. Généralement on encode les problèmes quantiques en binaire, c’est la manière la plus optimisée d’utiliser une série de bits. Cependant la modélisation des problèmes QUBO en binaire nécessite des portes quantiques complexes à utiliser en cadre réel (problème d’erreurs et de précision). Ainsi on encode ce genre de problème avec un encodage “one-hot”, cet encodage est plus couteux en qubit mais permet de simplifier grandement les portes utilisées. L’inconvénient de cette méthode est qu’il rend plus difficile l’implémentation de l’algorithme QAOA dans le cadre réel. L’un des composants principaux de l’algorithme, le “Mixer” (une combinaison de porte) devient complexe à créer mais aussi moins précis.
L’objectif de notre POC était de voir comment dépasser cette limitation de QAOA en utilisant des encodeurs. Grâce à ces encodeurs, on peut opter pour un encodage en one hot initialement et compresser les données en binaire pendant l’exécution du “Mixer”, cela permet d’obtenir l’efficience d’une compression en binaire, sans avoir à recourir à des portes logiques complexes. Le seul défaut étant que l’encodeur augmente le nombre de qubits nécessaire. Dans le cadre de notre POC nous avons utilisé QAOA pour résoudre le Graph Coloring problem sur simulateur. Nous avons testé la résolution de ce problème avec un QAOA classique puis avec l’amélioration proposé précédemment. Le résultat est incontestable (en simulateur on a 2 fois plus de précision pour le même nombre d’itération avec l’amélioration), l’amélioration de QAOA permet une meilleure précision en simulateur, donc représente un avantage conséquent pour un ordinateur quantique.
Simulateurs quantiques
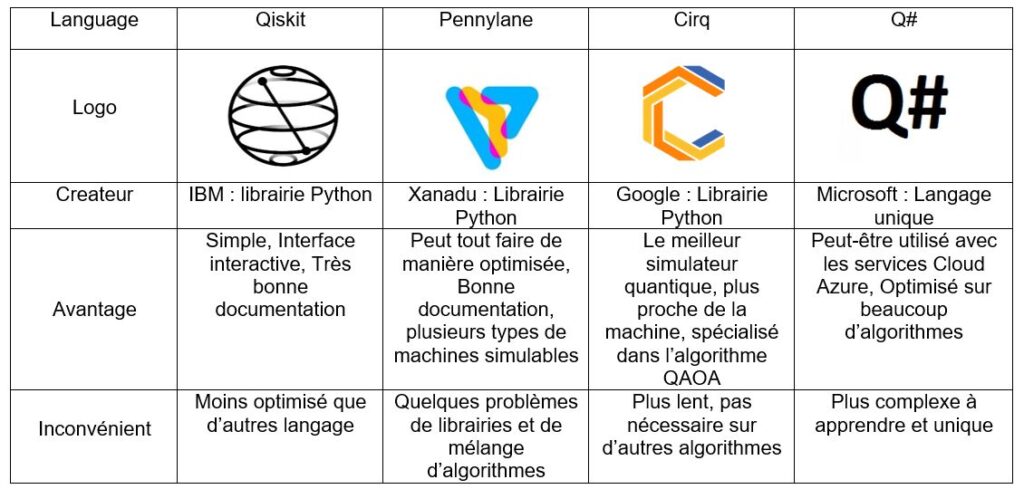
Afin de vous en apprendre plus sur les simulateurs, voici une liste de simulateur connus et de leur contexte d’utilisation :
Conclusion
Pour conclure, il est important de distinguer deux grandes classes d’algorithmes quantiques, les algorithmes plus anciens, qui présentent les gains de performance les plus impressionnants (comme Grover ou Shor) mais qui ne devraient pas être réalisables dans un avenir proche. Et les algorithmes récents comme QAOA, les algorithmes quantiques variationnels, algorithmes hybrides (exécutés avec l’aide d’une machine classique) qui permettent de réaliser des gains en utilisant les machines actuelles et présentent de nombreuses accointances avec le machine learning. Leur procédé d’optimisation est très similaire à celui du machine learning, et beaucoup d’algorithmes variationnels sont utilisés dans le cadre de l’IA, algorithmes pour réseaux de neurones, SVM, etc… Il sera donc très intéressant à l’avenir de suivre l’évolution de certains de ces algorithmes, d’autant que la recherche sur le domaine de l’informatique quantique est toujours en expansion.